# 4.3 回归问题评估
MAE、MSE和RMSE,是不同于类别预测,不能苛刻回归预测的数值结果要严格的和真实值一致。一般情况下,我们希望衡量预测值和真实值之间的差距。因此,可以通过多种测评函数进行评价。
# 4.3.1 平均绝对误差
Mean Absolute Error (MAE)
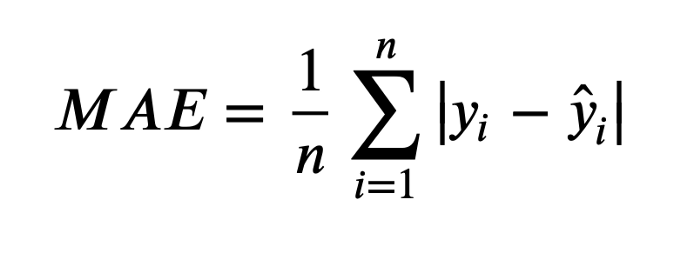
上面的公式中:n 为样本数量, y 为实际值, $\hat{y}$ 为预测值
MAE 越小模型预测约准确
Sklearn 中MAE的API
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test,y_predict)
# 4.3.2 均方误差
Mean Squared Error (MSE)
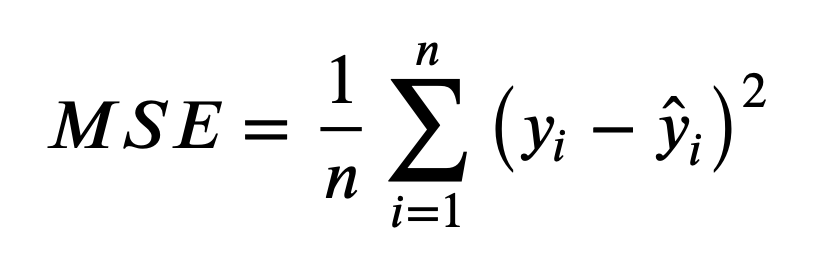
- 上面的公式中:n 为样本数量, y 为实际值, $\hat{y}$ 为预测值
- MSE 越小模型预测约准确
Sklearn 中MSE的API
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test,y_predict)
# 4.3.3 均方根误差
Root Mean Squared Error (RMSE)
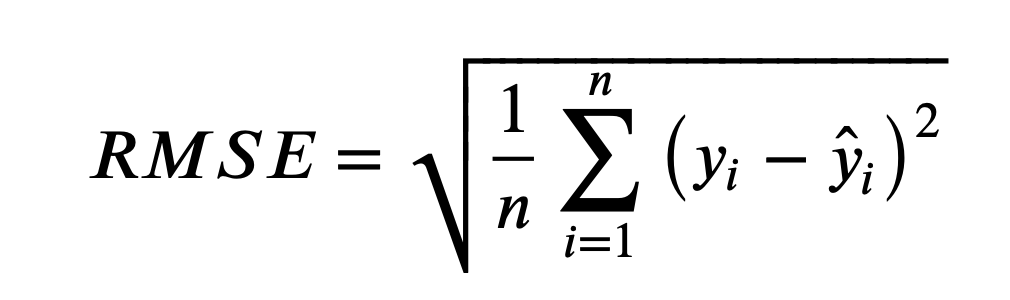
上面的公式中:n 为样本数量, y 为实际值, $\hat{y}$ 为预测值
RMSE 越小模型预测约准确
RMSE 是 MSE 的平方根。某些情况下比MES更有用,由于 MAE 和 RMSE 都是误差的一次方,可以将它们相互比较
# 4.3.4 三种指标的比较
看下面的例子
我们绘制了一条直线 y = 2x +5 用来拟合 y = 2x + 5 + e. 这些数据点,其中e为噪声
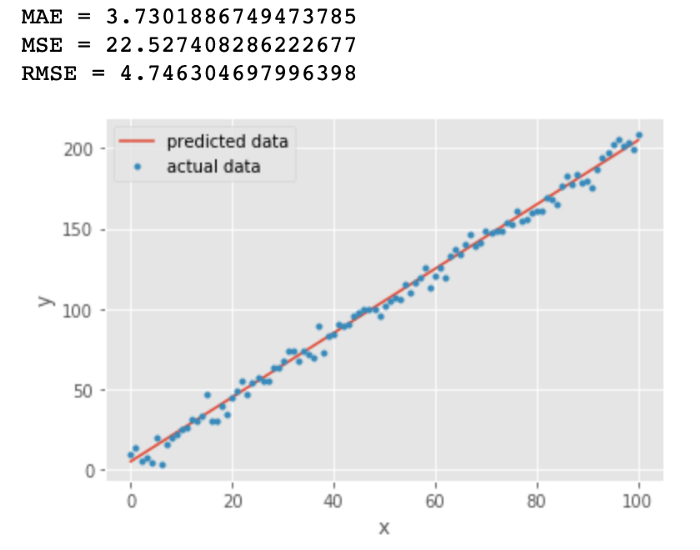
从上图中我们发现 MAE 和 RMSE 非常接近,都表明模型的误差很低(MAE 或 RMSE 越小,误差越小!)。 但是MAE 和 RMSE 有什么区别?为什么MAE较低?
对比MAE 和 RMSE的公式,RMSE的计算公式中有一个平方项,因此:大的误差将被平方,因此会增加 RMSE 的值
可以得出结论,RMSE 会放大预测误差较大的样本对结果的影响,而 MAE 只是给出了平均误差
由于 RMSE 对误差的 平方和求平均 再开根号,大多数情况下RMSE>MAE
举例 (1+3)/2 = 2 $\sqrt{(1^2+3^2)/2 }= \sqrt{10/2} = \sqrt{5} = 2.236$
我们再看下一个例子
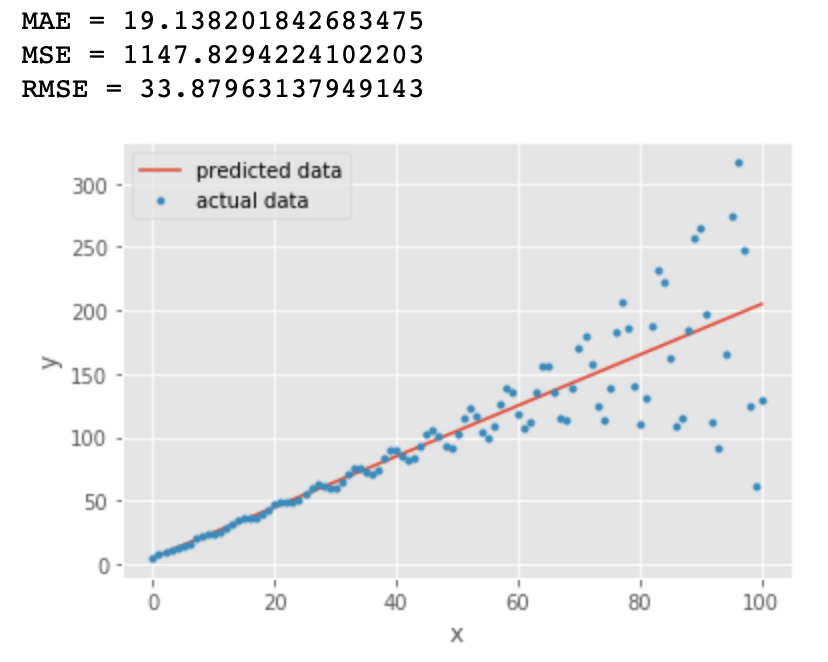
橙色线与第一张图中的直线一样:y = 2x +5
蓝色的点为: y = y + sin(x)*exp(x/20) + e 其中 exp() 表示指数函数
我们看到对比第一张图,所有的指标都变大了,RMSE 几乎是 MAE 值的两倍,因为它对预测误差较大的点比较敏感
我们是否可以得出结论: RMSE是更好的指标? 某些情况下(希望将小误差与大误差一样对待)MAE更有优势,例如:
- 假设数据中有少数异常点偏差很大,如果此时根据 RMSE 选择线性回归模型,可能会选出过拟合的模型来
- 在这种情况下,由于数据中的异常点极少,选择具有最低 MAE 的回归模型可能更合适
- 除此之外,当两个模型计算RMSE时数据量不一致,也不适合在一起比较
# 4.3.5 MAE, MSE and RMSE小结
一般我们使用MAE 和 RMSE 这两个指标
# 1. MAE、RMSE的优点
- 都能反映出预测值和真实值之间的误差
- MAE反应的是“真实”的平均误差,RMSE会将误差大的数据点放大
# 2. MAE、RMSE的缺点
- MAE 不能体现出误差大的数据点,RMSE虽然会加放大大误差的数据点对指标的影响, 但是对异常数据比较敏感
# 4.3.6 R-Squared 和 Adj. R²
# 1. R-Squared (R²)
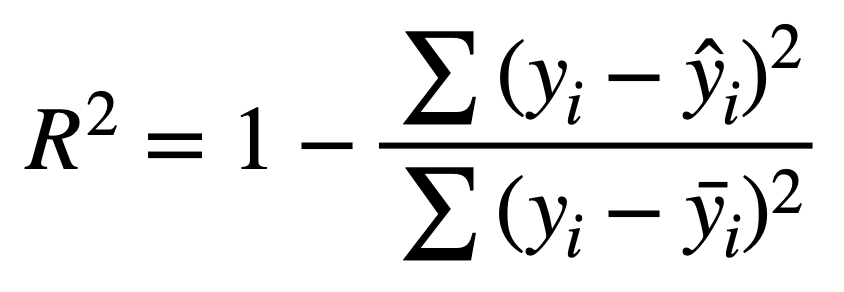
上面的公式中y = 真实值, $\hat{y}$ = 模型预测值, $\bar{y}$ = 真实值的平均值
Sklearn 中R-Squared 的API
from sklearn.metrics import r2_score
r2_score(y_test,y_predict)
R²代表了预测值和真实值拟合的拟合程度,既考虑了预测值与真实值的差异,同时也兼顾了真实值的离散程度
- R²<0.5 → 弱拟合
- 0.5 ≤ R² ≤ 0.8 → 中度拟合
- R² > 0.8 强拟合
注意:理论上 R² < 0 是可能的,但是只出现在模型特别差的情况,因此不予讨论
R² 只能代表拟合的强弱,但不能说R² 越大模型越好,如何理解?看下面的例子:
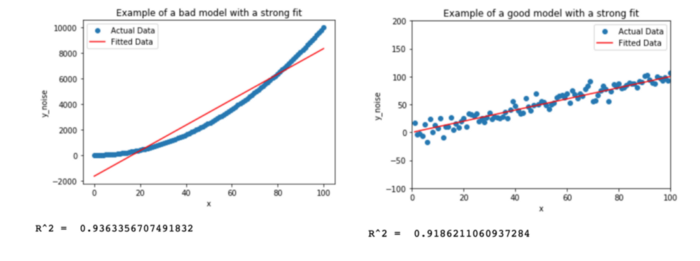
从R²值中可以看出,上图中两个模型属于强拟合的情况,它们的 R² 值都>0.9
但很明显,尽管左侧模型具有更高的 R² 值,但右侧模型是更好的模型。左边的模型很差,因为它无法捕捉到数据的曲率。因此,高 R² 并不意味着模型很好,它只是意味着实际点与拟合点的平均偏差很小。
有时,模型可能具有较低的 R² 值,但实际上却是不错的模型。看下面的例子:
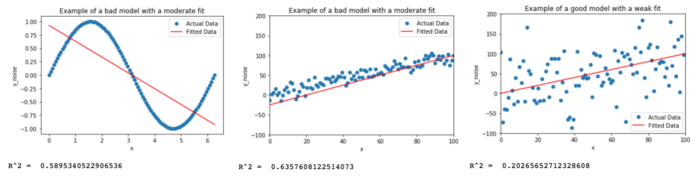
从上图中看出:
- 左侧模型的拟合度很差,但“拟合强度”适中
- 左侧模型与右侧模型相比,仅基于 R² 值,可能会认为最左侧的模型是更好的。这是错误的
- 再看中间模型,它的 R² 是右侧模型的三倍,并且从图中看出,似乎偏差不大,我们能否得出结论,中间模型比右侧型好得多?
中间和图右侧图中的 数据点 基于同一条线 y=x+e,其中 e 是服从正态分布随机生成的误差。它们之间的唯一区别是误差幅度在最右边的图表上被放大了
中间的模型红色的线实际上是如下模型:
y = 4.3.25*x-25
右边的模型是正确的,它的模型方程为: y = x,与生成数据点的线完全相同。
我们可以直观的看到,中间模型的直线有点儿偏
因此我们可以得出结论,具有低 R² 的模型仍然可以是好的模型,R² 较低的原因可能是数据方差较大
如果我们的目的是为了预测图中绘制出来的这部分数据点,那么中间模型可能会表现得更好,但这并不能说明中间的模型就是一个好模型(如果X取值增大,那么中间模型的误差会越来越大)
R² 小结
R² 指标表明模型与测试数据的拟合程度,但无法解释模型是否良好
某些情况下,当增加模型复杂程度(比如添加高次方项),R²值会变大,单独以R²作为评价指标,可能会导致过拟合
R² 对非线性模型没有意义
# 2. Adjusted R² (Adj. R²)
介绍R²时我们提到,当增加模型复杂程度(比如添加高次方项),R²值会变大,单独以R²作为评价指标,可能会导致过拟合,我们可以通过Adj. R²来解决这个问题
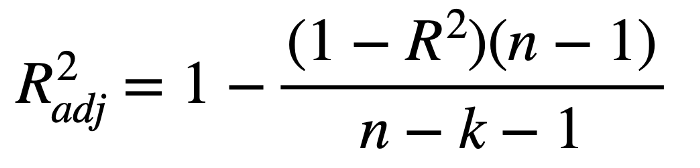
上面的公式中,n 为样本数量,k 为模型中的自变量数,不包括常数项(截距)
比如:y =a0 + a1*x1 + a2*x2 对于这个模型 k = 2
为什么adjusted R-squared 比R-squared好? 接下来我们考虑如下两个模型:
y = x
y = a0+a1*x1+a2*x²²+a3*x³³+a4*x⁴⁴+a5*x⁵⁵+a6*x⁶⁶+a7*x⁷⁷
我们用上面两个模型分别拟合由 y=x+e 表示的数据,图形如下所示

如图上图所示:
- 左侧模型(有更多项高次方项)的 R² >右侧模型,单看R²指标左侧模型更好,但数据是基于 y=x+e 生成的
- 当我们查看Adjusted R² 值时,会发现最右边模型的R² 值 与 Adjusted R² 差值很小
- 左边模型R² 值 与 Adjusted R² 差值明显,说明左边模型过拟合了
为了验证这个结论,依然使用 y=x+e 产生数据,只不过重新生成一组随机数e ,再次用上面两个模型拟合新数据
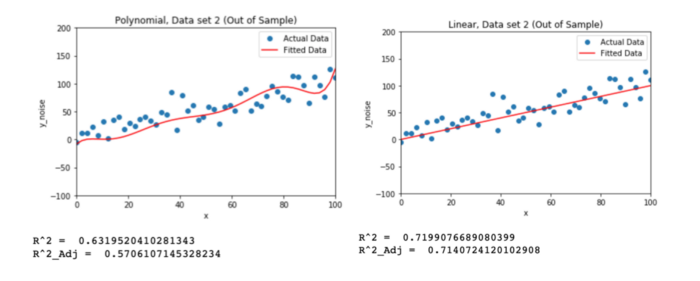
从上面的结果中看出,新的数据中,简单模型的R² 值 与 Adjusted R² 都没有太明显的变化, 但是复杂模型的R² 值 与 Adjusted R² 都有明显的减小,说明复杂模型之所以在第一组数据集中表现良好,是因为拟合的是数据的噪声
因此,同时使用R² 与 Adjusted R² 可以更好的对模型是否过拟合做出判断,但更靠谱的办法还是使用多组不同的测试数据对模型进行测试。
Adjusted R² 小结
通过Adjusted R² 可以在R² 的基础上对模型是否过拟合提供更多的信息
# 4.3.7 小结
常用的回归问题的评估方法
- MAE, MSE 和 RMSE
- R² 与 Adjusted R²
MAE, MSE 和 RMSE
- RMSE会放大预测误差较大的样本的影响
- MAE对误差大小不敏感
- RMSE对异常数据敏感
R² 与 Adjusted R²
- R²<0.5 → 弱拟合
- 0.5 ≤ R² ≤ 0.8 → 中度拟合
- R² > 0.8 强拟合
不能单独通过R²的大小来判断模型好坏,可以通过配合Adjusted R² 和 多用不同的测试数据来修正R²的不足
← 4.2 特征工程 5.1 垃圾邮箱分类项目 →